一起学AI 3.通过一个例子重新认识AI

回顾总结

前三篇文章主要介绍了写“一起学AI”专栏的初衷、AI的历史和构成以及数学的历史和分支。

旨在帮你形成完整的知识体系。

但像这种综述性的文章本就不好写，它需要作者有很“广”的知识储备，以及很“深”的见解才能让文章的内容丰富饱满，且结构性、逻辑性更强。这样在读完之后才会在脑子里形成一张图。

受限于作者的能力，仅通过这三篇文章似乎很难达到预想的效果，若您此刻仍感迷雾重重,不妨忘却所有细节,仅记住下面这两张图就好了。

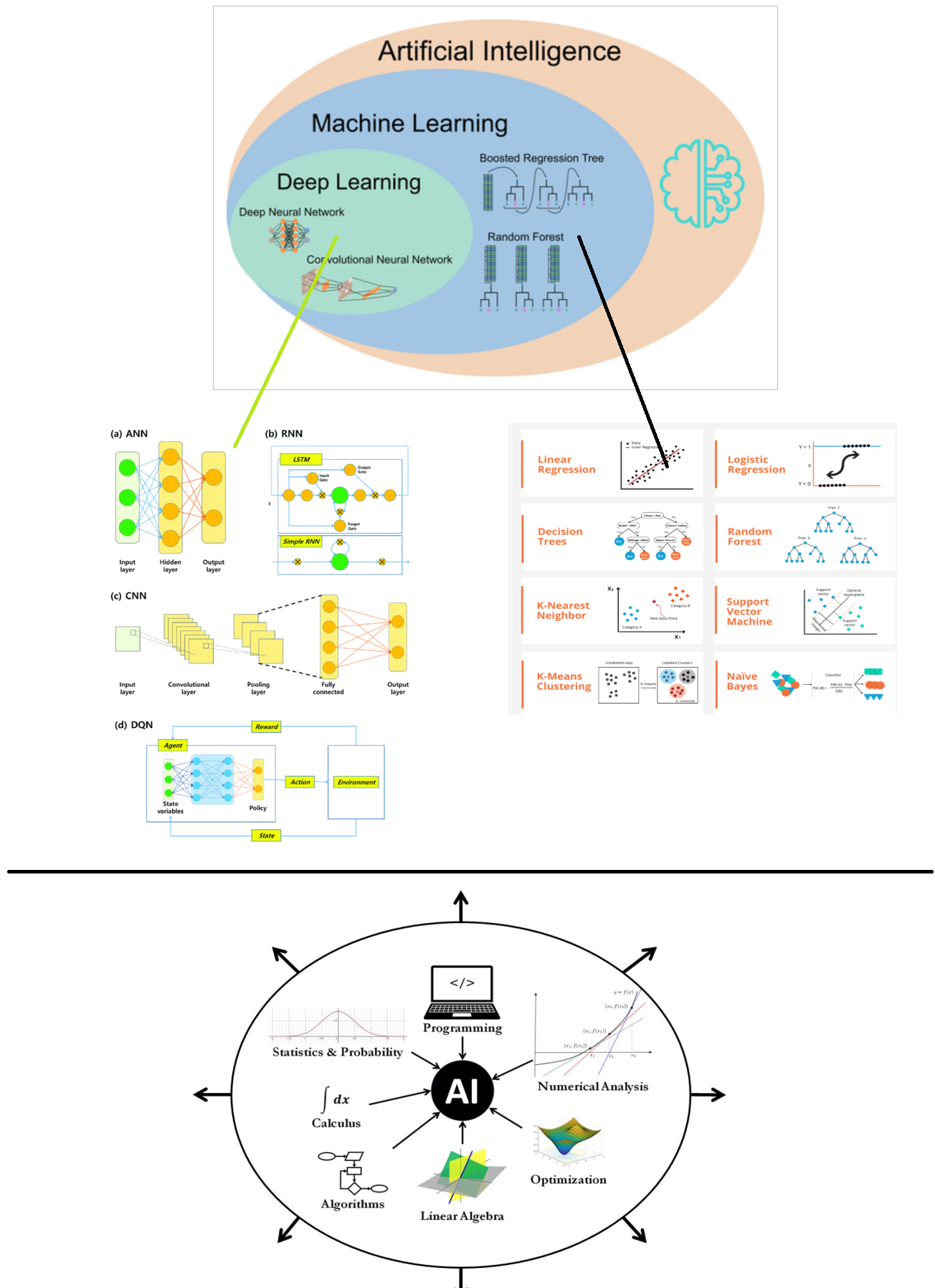
图1 AI构成：下面是数学原理，上面是AI应用

上面这张图描述了AI的静态结构，当您充分理解以后，就可以继续分析下面这张动态训练图。

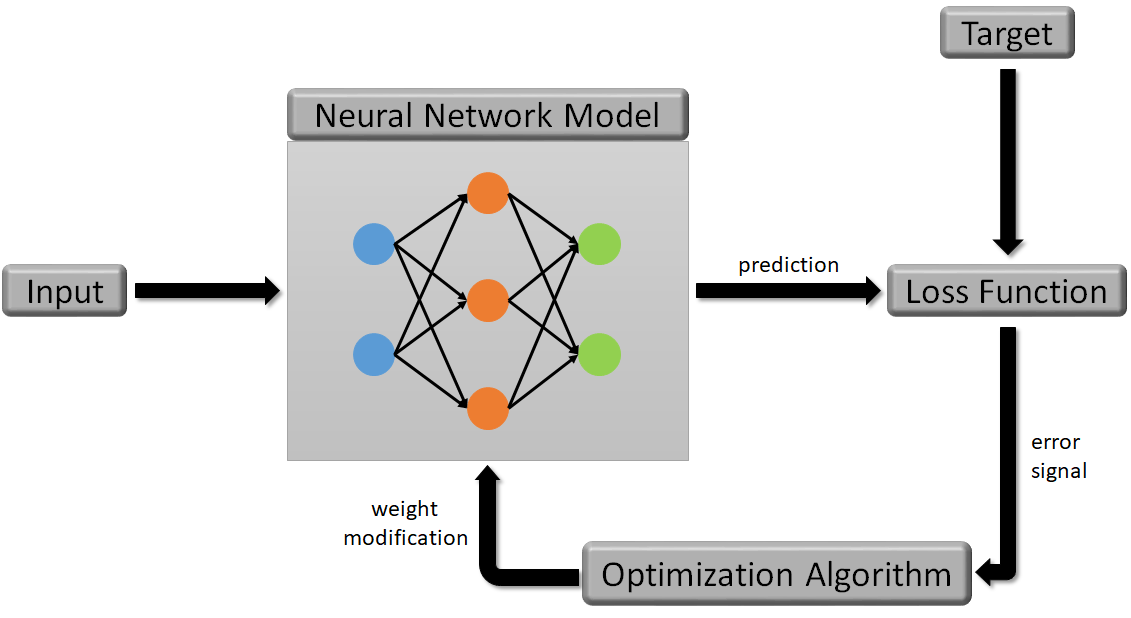
该图清晰描绘了AI三驾马车（模型，优化算法，损失函数）在训练过程中是如何相互作用的，无论是传统机器学习还是深度学习，模型架构可能有所差异，但训练流程基本类似,。

图2 模型的训练流程

一个具体的例子

如果前面的文字和图片仍未解开您所有的疑惑,不妨我们换个思路，从零开始用python代码实现一个模型，使其尽可能涵盖所有关键概念。

首先明确具体需求——我们希望AI完成什么任务？为便于演示，本文选择一个简单的二分类任务。

除二分类外,常见任务还包括多分类、线性回归。

在计算机视觉领域有图像分类、目标检测、图像分割。

在自然语言处理领域有文本分类、总结、生成等。

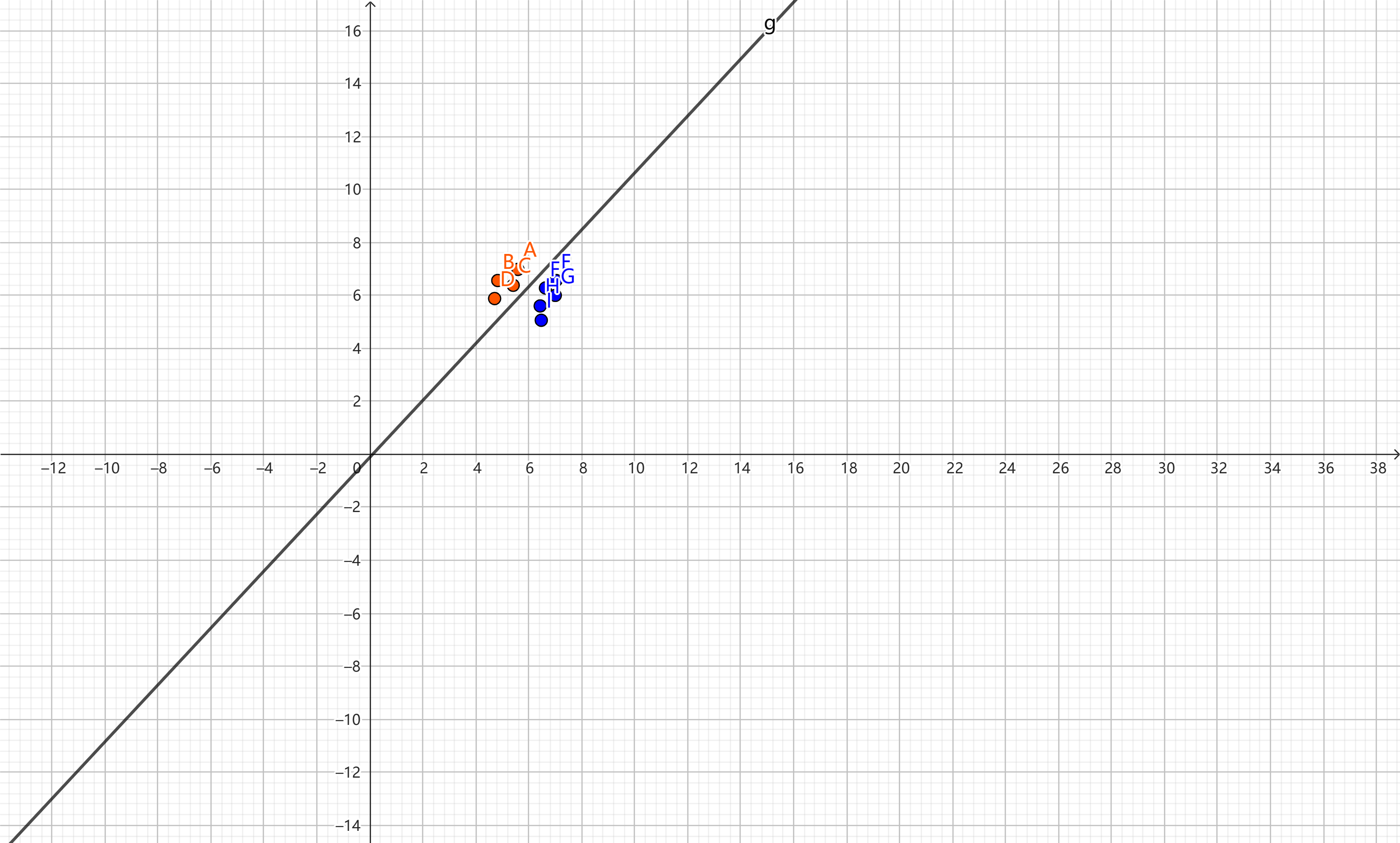
第二步准备数据。

alt

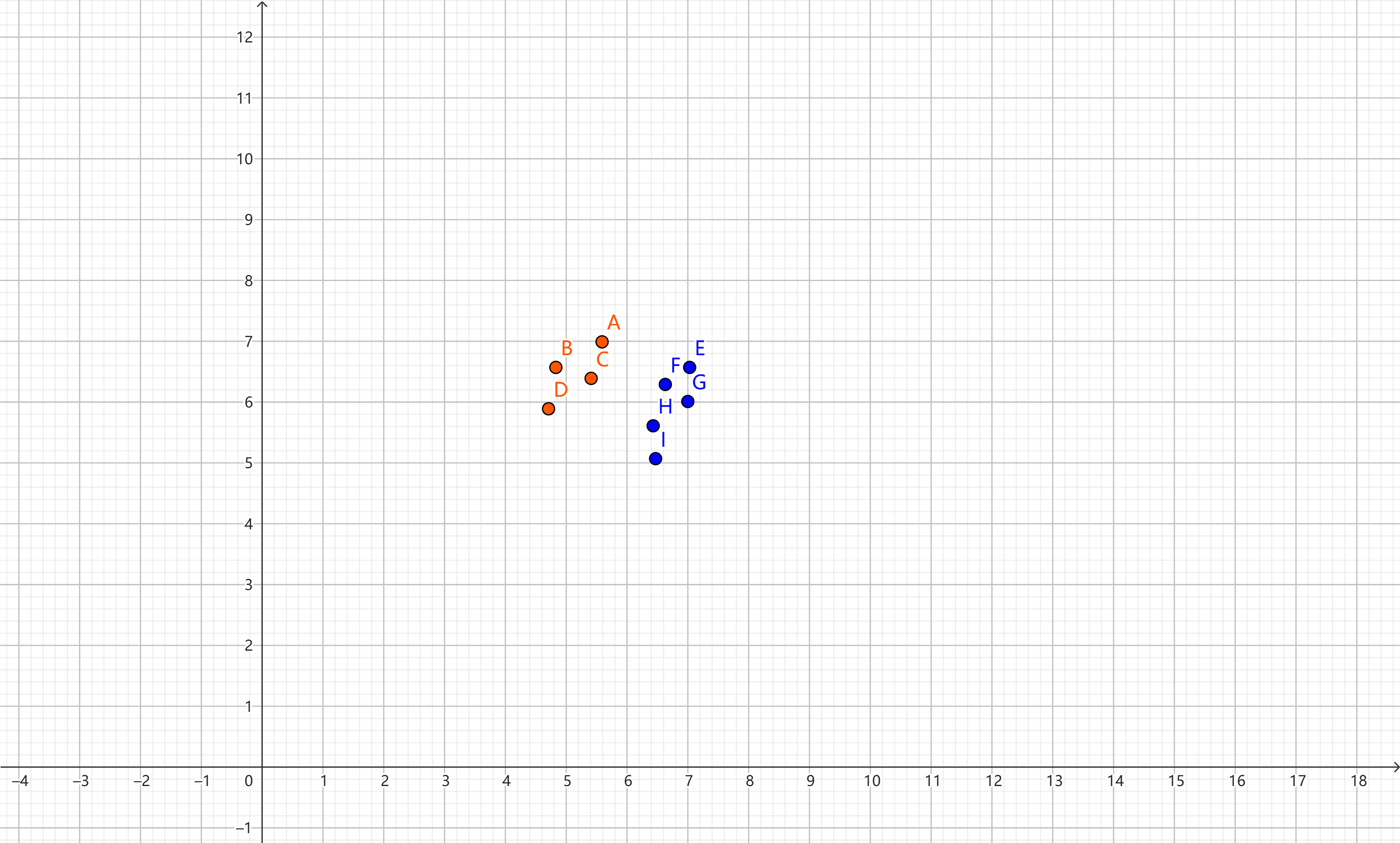
红色的点代表正样本y=1，蓝色的点代表负样本y=0，水平轴$x_{1}$和垂直轴$x_{2}$代表特征。

这种数据我们也称为表格数据，除此之外，还有图像、文本、图数据。

x1	x2	y
5.59	6.98	1
4.83	6.56	1
5.41	6.38	1
4.71	5.88	1
7.03	6.56	0
6.63	6.28	0
7	6	0
6.43	5.6	0
6.47	5.06	0

无论是机器学习还是深度学习，在开始训练之前通常需对数据进行预处理。

如果是表格数据，则需要将文字特征(是，否)数字化(One-hot Encoding)，处理缺失数据(删除或插值填充)，通过相关性分析删除与分类结果无关的特征(低相关性过滤)，删除重复或高度相关的特征(高相关性过滤，去重复)，并进行归一化(Min-Max Scaling ， Z-Score 等)来加快模型收敛以及消除量纲的影响。

如果是图像,为了提升模型的泛化性能，就需要给模型看更多内容更丰富的数据，这就需要通过旋转,缩放,裁剪,颜色变换等操作扩增数据，同样图像也需要归一化(减均值除以标准差)。

对于一些特殊领域的图像，例如，医疗图像可能还需要窗宽窗位的变换。

如果是文本,则需要 tokenize 或 word embedding(Word2Vec, Glove, BERT 等)。

为简化过程,本文将忽略数据预处理这一步。

data = [[5.59,6.98,1], [4.83,6.56,1], [5.41,6.38,1], [4.71,5.88,1],[7.03,6.56,1],[6.63,6.28,1],[7,6,1],[6.43,5.6,1],[6.47,5.06,1]]
X = np.array(data)
label = [1,1,1,1,0,0,0,0,0]
y = np.array(label)

第三步,去图1中挑选一个适合任务的模型。许多模型都可完成此二分类任务,如逻辑回归、SVM、决策树、随机森林、Adaboost等传统机器学习模型；也可以使用深度学习中的ANN(前馈神经网络)模型。

对于模型的选择，通常情况下深度学习模型要比传统机器学习拟合能力更强，但这并不意味着无论什么任务只要选择深度学习就好了，模型复杂度和数据量要成比例，如果初期数据量不多，传统机器学习可能是更好的选择，等到数据积累够了，再迁移到深度学习也不迟，所以，总结一下就是：不求最贵，但求最好。

为简便起见，本文选择最简单的逻辑回归模型。

如前所述,模型的作用是将输入映射到输出。对二分类任务而言,模型只需输出样本属于正类的概率。

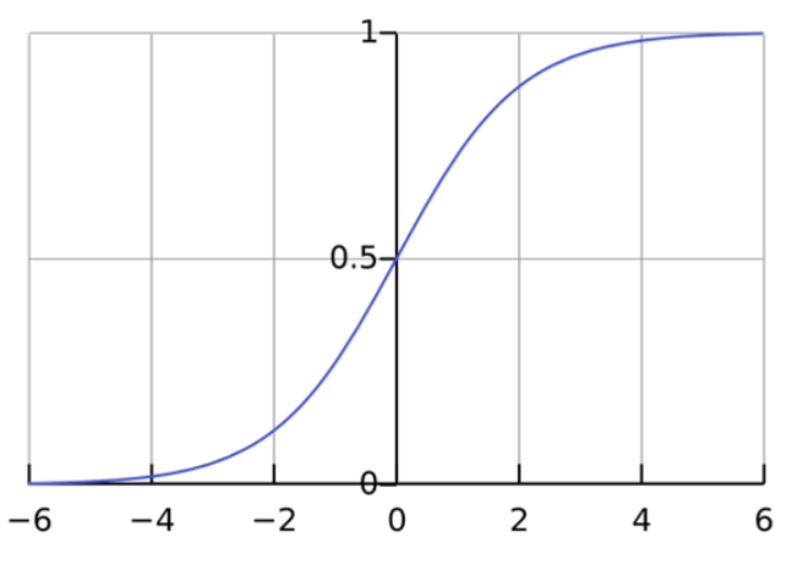
有人发现sigmod函数的性质正好满足这个要求。

$$ f( x) =\frac{1}{1+e^{x}} $$

sigmoid 函数的输出界于 0-1 之间,符合概率的性质。当 x 大于 0 时,函数输出也将大于 0.5。根据设定,输出超过阈值0.5 即可判断该样本属于正样本类。

alt

因为数据有两个特征，所以模型可以写成下面形式：

$$ f( x_{1} ，x_{2}) =\frac{1}{1+e^{-( w_{1} x_{1} +w_{2} x_{2} +b)}} $$

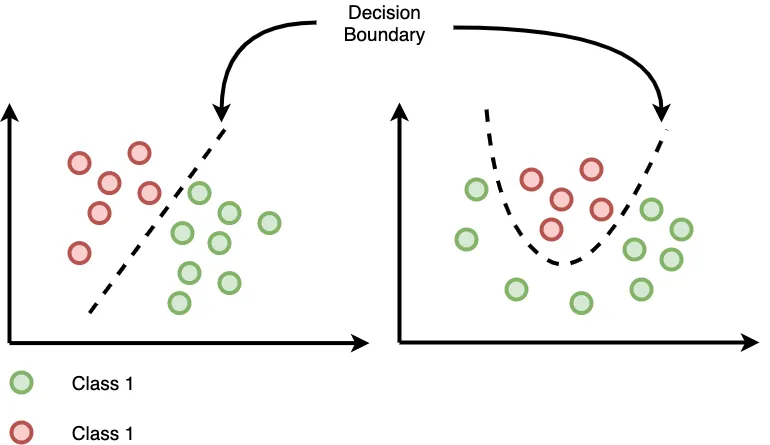
根据sigmod函数的性质，如果$w_{1} x_{1} +w_{2} x_{2} +b\ >0$就可以判定为正样本.

换句话说，分类器的决策边界就是$w_{1} x_{1} +w_{2} x_{2} +b\ \ =0$这条直线，这样的分类器被称为线性分类器，如果数据线性不可分，则也可以使用非线性函数，例如，多项式函数。

alt

更进一步地，可以将上面公式转换成向量形式。

$$ f(\vec{x}) =\frac{1}{1+e^{-\vec{w}^{T}\vec{x}}} $$

$\vec{x} =[ x_{1} ,x_{2} ,1] ,\vec{w} =[ w_{1} ,w_{2} ,b]$均为列向量。

这样我们就已经进入到线性代数的领域，然后用线性代数中的工具进行计算了。

向量$\vec{w}$就是要求解的参数，所谓机器的智能，在很大程度上源自其通过学习参数拟合函数的能力。

# 用theta表示模型的参数W
theta = np.zeros(3)
# 逻辑回归模型
def sigmoid(x):
    return 1 / (1 + np.exp(-x))

第四步开始训练

根据图2可知，模型的训练过程可以概括为：通过优化算法迭代更新模型参数,以最小化预测结果与真实标签之间的损失函数值。

模型我们已经有了，就是前面的逻辑回归函数，现在就差损失函数和优化算法了。

首先要选择损失函数，对二分类任务,每个样本仅属于正负样本中的一个类别。对于第i个样本，如果是正样本，概率为$f( X_{i})$,如果是负样本，因为sigmod函数输出的是属于正样本的概率，所以概率为$1-f( X_{i})$

因为所有样本都是独立同分布的，所以对于整个训练数据集来讲，整体概率为单个样本的乘积。

$$ L(\vec{w}) =\prod_{i=1}^{i=k} f( X_{i})\prod_{i=k+1}^{i=n}( 1-f( X_{i})) $$

X是所有训练数据组成的矩阵，$X_{i}$表示第i个样本的特征向量。

n为训练样本总数，k为正样本个数。

这实际上就是概率与统计中的似然函数，“似然”就是可能性的意思，通过最大化似然函数来求得参数的值就是最大似然估计，也就是求得参数W使得L(W)取得最大值。

$$ Max_{\vec{w}} L(\vec{w}) $$

因为标签$y_{i}$要么是0，要么是1，所以上面的似然函数可以进一步写成下面形式。

$$ L(\vec{w}) =\prod_{i=1}^{i=n} f( X_{i})^{y_{i}}( 1-f( X_{i}))^{1-y_{i}} $$

多个指数函数的乘积不方便求解。我们可以对其取自然对数,将乘法转换为加法。

由于目标是求函数最大值,可以将函数乘以-1后转化为求最小值问题。同时,对于n个数据,累加值可能非常大,使用梯度下降时则易导致梯度爆炸。为避免这一问题,可将累加式除以样本总数n进行归一化，它也被称为对数损失函数。

$L(\vec{w}) =\frac{1}{n}\sum\limits_{i}^{n} -y_{i} f( X_{i}) -( 1-y_{i}) ln( 1-f( X_{i}))$

如果你了解交叉熵损失函数，那么，上面的公式是不是就很熟悉了？其实，经过证明，逻辑回归中,使用交叉熵损失函数求解参数和使用最大似然估计求解参数,在数学上是等价的。

现在我们的目标就是求得参数W使得L(W)取得最小值。

$$ Min_{\vec{w}} L(\vec{w}) $$

# 损失函数    
def compute_loss(X, y, theta):
    y_pred = sigmoid(X.dot(theta))  
    loss = -np.mean(y*np.log(y_pred) + (1-y)*np.log(1-y_pred))
    return loss

这时该优化算法出场了，在训练开始时，先随机初始化参数，然后利用梯度下降进行迭代更新。

alt

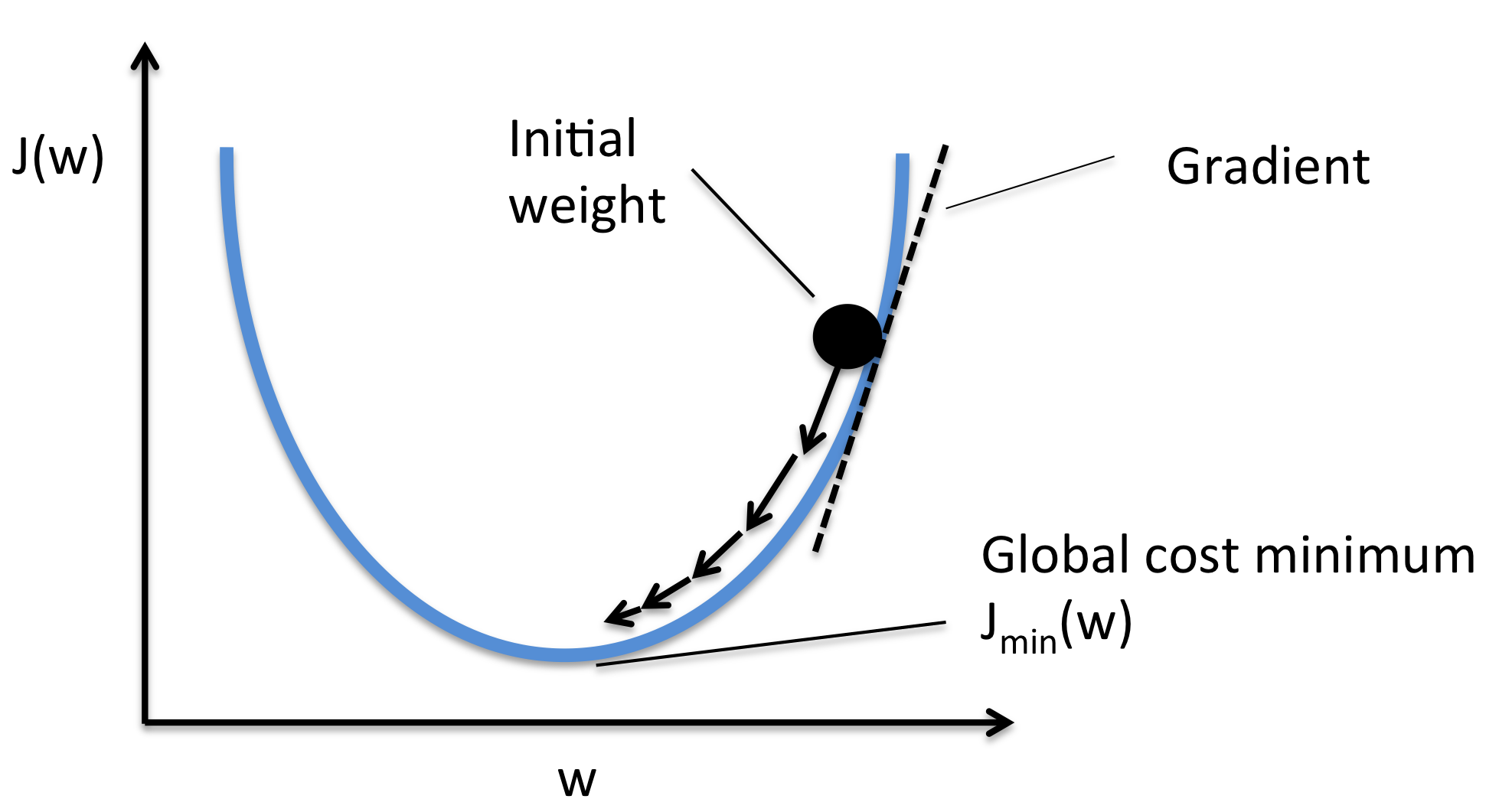
首先需要L(W)对w求偏导数。

$$ \frac{\partial L(\vec{w})}{\partial \vec{w}} \ =\sum\limits_{i}^{n}( f( X_{i}) -y_{i}) X_{i} $$

最后对参数进行更新：

$$ \vec{w} _{t+1} =\vec{w} _{t} \ -\ learningrate* \frac{\partial L(\vec{w})}{\partial \vec{w}} $$

# 梯度下降    
for i in range(num_iterations):
    y_pred = sigmoid(X.dot(theta))
    gradient = X.T.dot(y_pred - y) / 9
    theta = theta - learning_rate * gradient
    loss = compute_loss(X, y, theta) 
    print(f"Iteration {i}: Loss {loss:.3f}")

训练10000轮后，最终得到参数W=[-3.94707138 3.6713051 0.40745513],最后一个是b。

其中，训练的轮数以及学习率都是超参数，可以通过经验获得，也可以通过AutoML得到，这个后续我们还会详细介绍。

alt

完整代码：

import numpy as np
​
data = [[5.59,6.98,1], [4.83,6.56,1], [5.41,6.38,1], [4.71,5.88,1],[7.03,6.56,1],[6.63,6.28,1],[7,6,1],[6.43,5.6,1],[6.47,5.06,1]]
X = np.array(data)
​
label = [1,1,1,1,0,0,0,0,0]
​
y = np.array(label)
​
print(X.shape)
​
# 参数初始化
num_iterations = 10000
learning_rate = 0.01
theta = np.zeros(3)
# 逻辑回归模型
def sigmoid(x):
    return 1 / (1 + np.exp(-x))
# 损失函数    
def compute_loss(X, y, theta):
    y_pred = sigmoid(X.dot(theta))  
    loss = -np.mean(y*np.log(y_pred) + (1-y)*np.log(1-y_pred))
    return loss
# 梯度下降    
for i in range(num_iterations):
    y_pred = sigmoid(X.dot(theta))
    gradient = X.T.dot(y_pred - y) / 9
    theta = theta - learning_rate * gradient
    loss = compute_loss(X, y, theta) 
    print(f"Iteration {i}: Loss {loss:.3f}")
​
​
print(theta)

本例中我们只有训练数据集，但为了评估模型的泛化性能,通常需要将数据集划分为训练集、验证集和测试集。训练集用于训练模型,验证集用于调参和选择模型,测试集最终评估模型效果。

在简单问题上,训练数据可完美拟合,但实际情况复杂许多。模型容易过拟合或欠拟合。这需要采取正则化、增强数据、 Ensemble等手段提高模型鲁棒性,同时在验证集上监测并相应调整模型结构与超参,从而在测试集取得更优泛化性能。

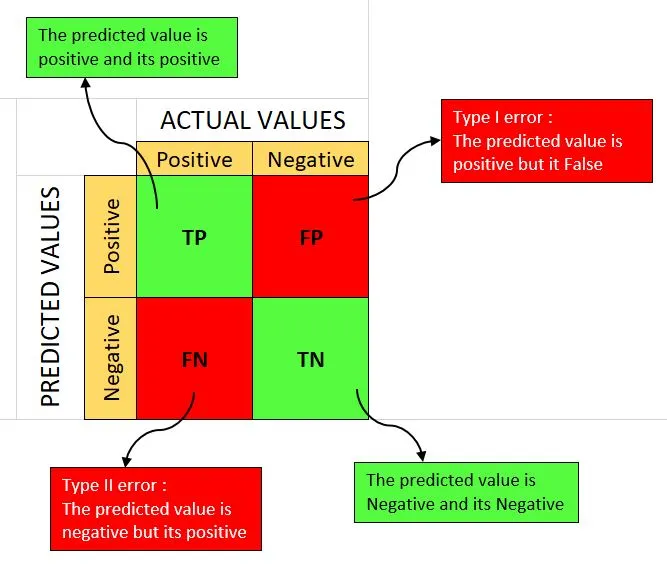
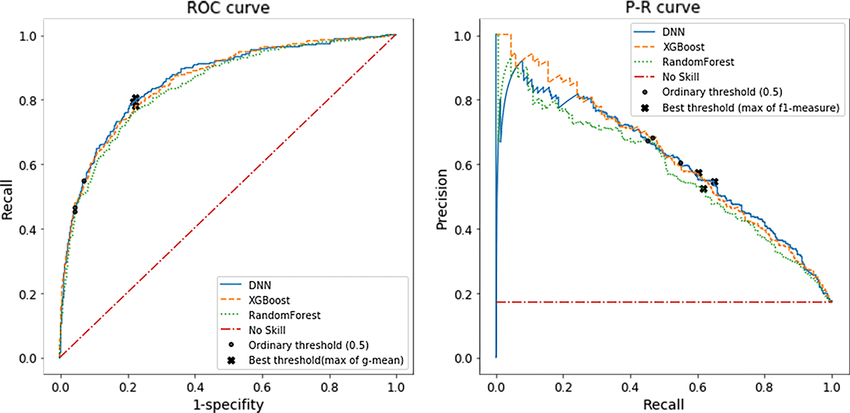
对于分类任务，不同的阈值，同一个样本可能会被划分为不同的类别，如何选择合适的阈值呢？可以借助模型的评估指标，例如，通过绘制模型在不同阈值下的PR曲线或者ROC曲线来选择合适的阈值。

alt

展望未来

如果通过前面的文章能够形成完整且清晰的知识体系，那么后面展开的细节精讲就会容易很多，磨刀不误砍柴工。对于如何精讲，同样面临两种选择——自底向上或自上而下。

传统教学往往采取自底向上的方法，先建立数学基础，再介绍具体模型与应用。就像建造房屋，先打好地基。

这虽然符合人的直觉，但对AI学习来说，我认为后者会更为实用。我们并不需要完整掌握深奥的数学原理才能进入AI应用的大门。事实上，许多成功的AI从业者都是从实际问题出发，根据遇到的困难与需求来驱动对理论知识的学习。

网上对于调参侠的看法我也不是很赞同，在AI的从业之路上大多数人都得经过调参侠这一过程，也只有弄明白AI是什么之后才能跃迁到下一个等级。

所以,后续的内容我会采取自上而下的方法,从应用入手,需要时再探索原理。这样既可快速建立实践能力,又不失去深入理解的动力。

上面我们从0开始实现了一个二分类模型，实际上，使用机器学习框架仅用2行代码就能完成上述任务。

# 创建逻辑回归分类器
log_reg = LogisticRegression()
# 拟合训练集数据
log_reg.fit(X_train, y_train)   

下一篇文章我会介绍一些常用的AI工具框架，以及如何使用大模型来提升工作效率，正所谓工欲善其事，必先利其器。