一起学AI 2.数学的迷

如果你爱一个人，叫他去学数学吧！ 可以直上天堂. 如果你恨一个人，叫他去学数学吧！ 可以直下地狱.

小学，初中，高中，大学所学的数学

让我们一同回顾从小到大学过的数学，帮你唤起“美好”的回忆。

小学数学

当我来到低年级的教室旁，我总会听到“1、2、3、4、5”的朗读声，这是老师在教学生认识数字。

数字的全称应该是阿拉伯数字，起源于公元5世纪左右的古印度的数字系统,通过阿拉伯文化的传播,最终成为了全世界共同使用的数字语言。

但阿拉伯数字并不是唯一的数字语言，在同时期或者在其之前还有其它数字系统。

罗马数字：如I表示1,V表示5,X表示10等。

算筹:中国古代的结绳计数。

印度-婆罗米数字:阿拉伯数字的前身，但不包括0。

除此之外，还有玛雅数字，古埃及数字。

如果阿拉伯数字没有统一数字语言，所有数字语言各自为营的话，各国之间的贸易交流很难想象会是什么样子。

而在古老的中国，一位千古帝王同样意识到了这一点，他就是秦始皇，所以才有了车同轨，书同文，统一度量衡。

当我沿着走廊往前走，来到更高年级教室，我会听到“1 1得1、1 2得2”的朗读声，这是老师在教授算数运算。

这是我(80后)上小学时常用的两个工具，随着计算机的普及这些早已成为历史了吧！

当我来到更高年级的教室，我发现每个学生的桌子上都摆着一个工具盒，里面有三角板，圆规，尺子，这是老师在教授简单的几何形体和图形，帮学生认识点、线、面、体的基本概念。

而几何学的起源可以追溯到公元前3000多年的古埃及和古巴比伦时期，用于测量土地。

当我来到更高年级时，黑板上画了很多统计图表，这是老师在教授简单的统计与数据表示。

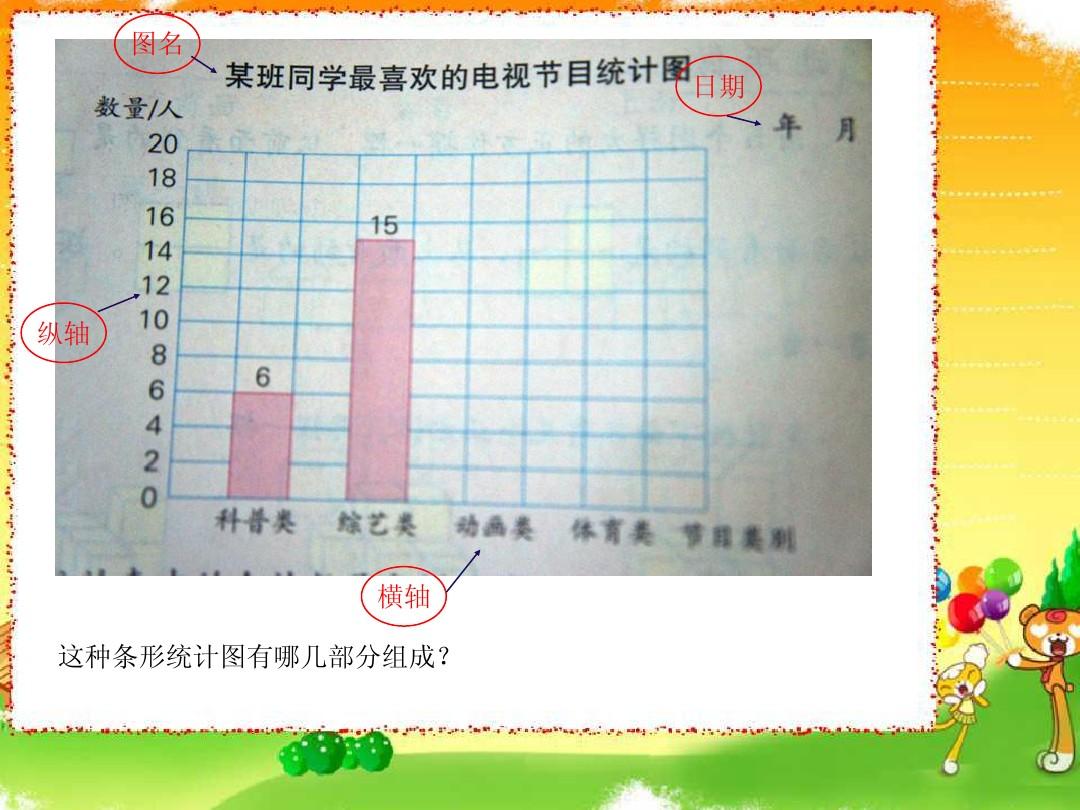
统计学的起源可以追溯到17世纪中叶，为了国家调查、人口普查等需求而产生。其主要包括两部分：概率论和统计学。

概率论：以数学方法描述和分析不确定性。

统计学：从样本中推断出总体特征并进行决策。

马斯克和任正非先生都曾说过：AI就是统计学。可见我们从小学就已经接受AI教育了。

我们姑且认为一个成功企业家说什么都是对的，毕竟他们是从战略角度描述问题，但作为搞科学研究的还是要较一下真，后面我们也会给出统计学和AI的一些些许差别。

好了，到此恭喜你已经小学毕业了，你将开启初中生活。

初中数学

在小学时，你已经对数字有了基本的认识，但这远没结束，数学的深奥与庞大就像一个迷一样。

上初中后老师会对数字进一步划分：自然数、整数、分数、小数，以及对应的四则运算。

上图中我们按照某种性质将数字划分为自然数，全体数，整数，有理数，并且通过元素的共性建立起交集的关系，这其实已经有了集合和逻辑的概念，集合就是具有某种共同性质的元素组成的整体。

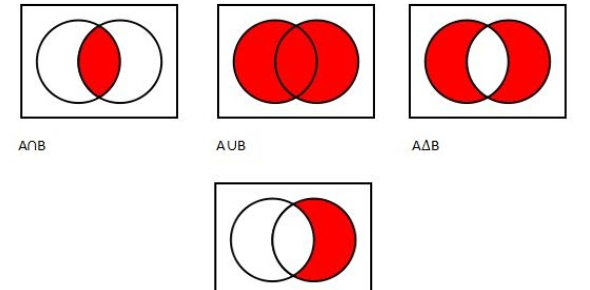
此时你也已经具有探索世界的未知的认知能力了，这类似于初中代数所涉及的内容，例如一元一次方程和二次方程的求解。

代数思想早在古埃及和巴比伦时期就有了。

在初中时期学习的是初等代数，其中未知数和系数均为有理数。大学时将继续学习高等代数，高等代数研究的是系数和未知数可以是任意数的方程或方程组。举例来说，在大学的线性代数中，未知数和系数则被表示为向量和矩阵。

同样，在小学时期学的几何学在初中也会进一步扩展，这时会研究这些几何形体的更高级性质，例如，三角形合同、圆的理论知识,学习利用公理证明定理。

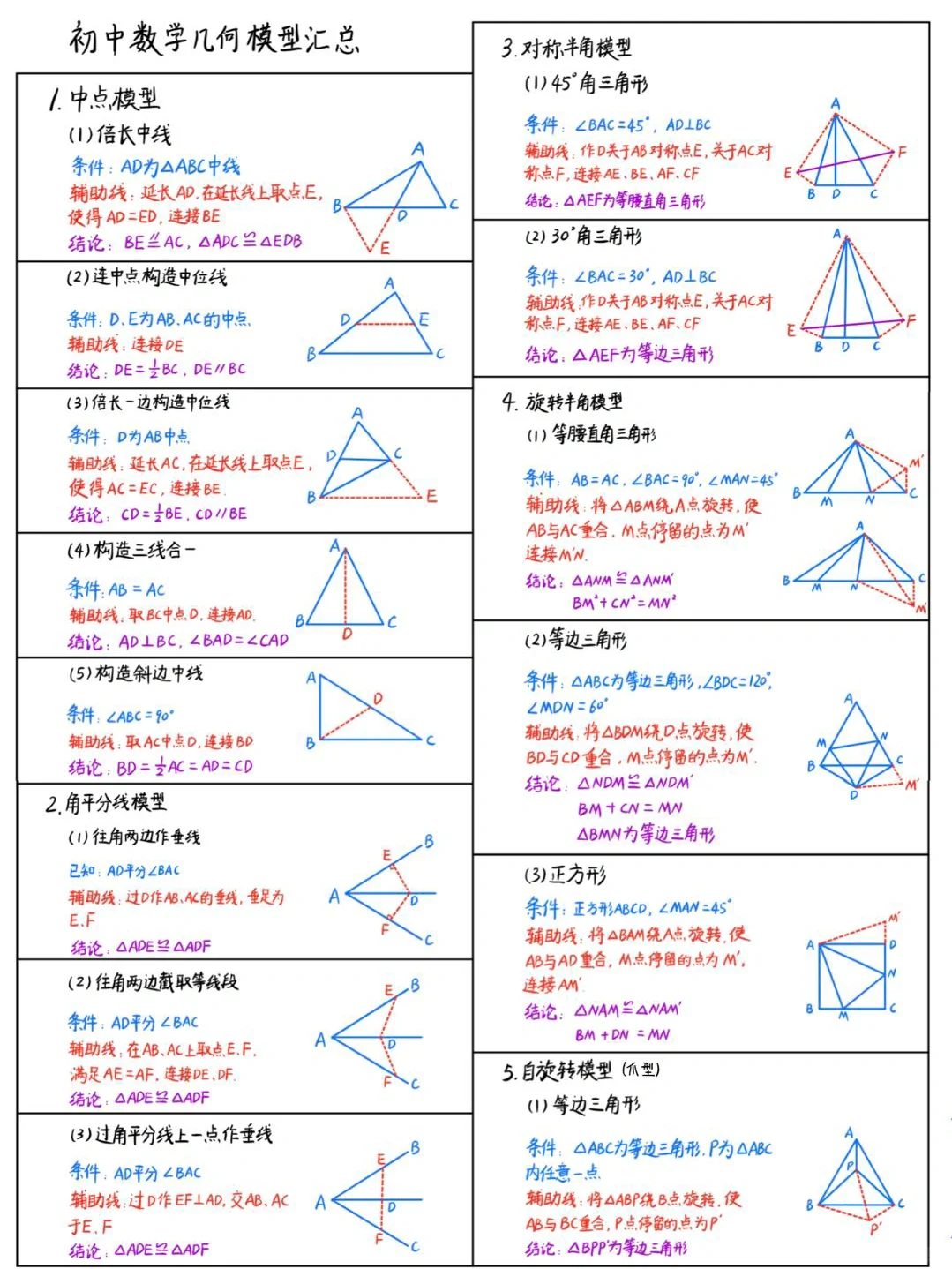
在初中我们也将学会概率的计算以及学习更多的统计方法，例如计算平均数和方差以及简单的数据可视化方法。

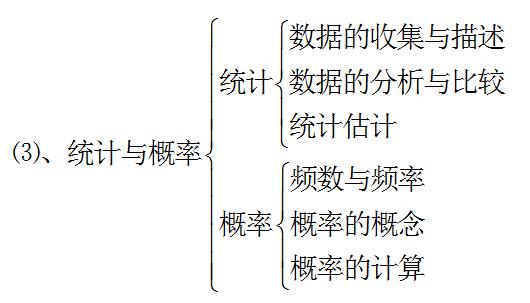
好了，到此，义务教育结束了，随着教育的重要性日益凸显，越来越多的人认识到它是改变命运的最佳途径，所以很多人会继续读高中。

高中数学

上高中后，逐步迈向成年，摆脱稚嫩，已经形成独立思考的能力，能够根据环境变化做出决策。

这种能力就类似于高中时所学的函数，函数的本质就是将输入映射成输出。

这个过程的决定权也掌握在我们自己的手中，导数像是飞快掠过的青春,积分则更像是逐步积累的人生。

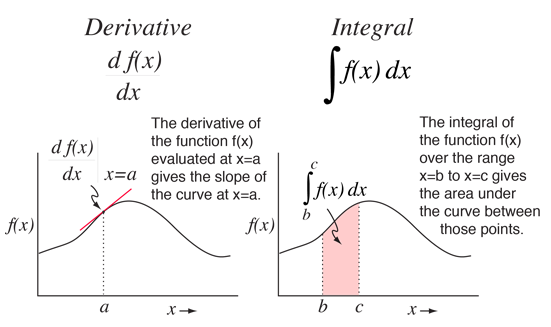
AI的核心是学习一个函数,使其描述输入和输出之间的映射关系,进而完成指定预测任务。这里,函数就是AI三驾马车中的模型。

要优化模型,这就涉及微积分的知识了，首先需要目标函数来评价模型效果的好坏，具体来说,我们构建描述模型误差的目标函数。然后利用其导数指引参数迭代更新的方向——这个思路被称为“梯度下降”。

这就好比下山，只要沿着坡度最陡峭的方向往山下走就好了。而这个方向就是利用函数的导数确定的，这种方法也被称为梯度下降法。

如果函数自变量是标量，我们称之为导数。

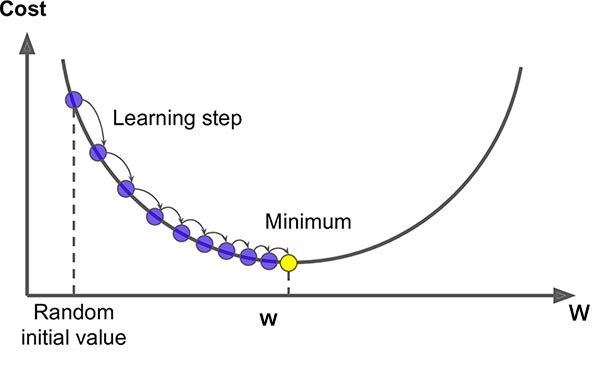
如果自变量是高维度的向量或者矩阵，则称之为偏导数。

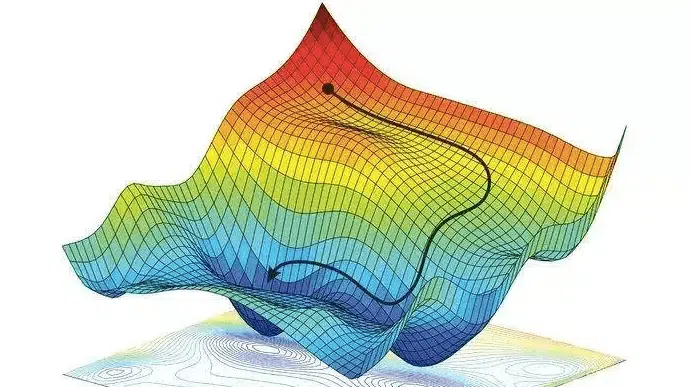
在高中，你将继续学到更高级的几何学内容，其中解析几何主要研究平面曲线与圆的性质,空间几何着重立体图形的计算与理解。

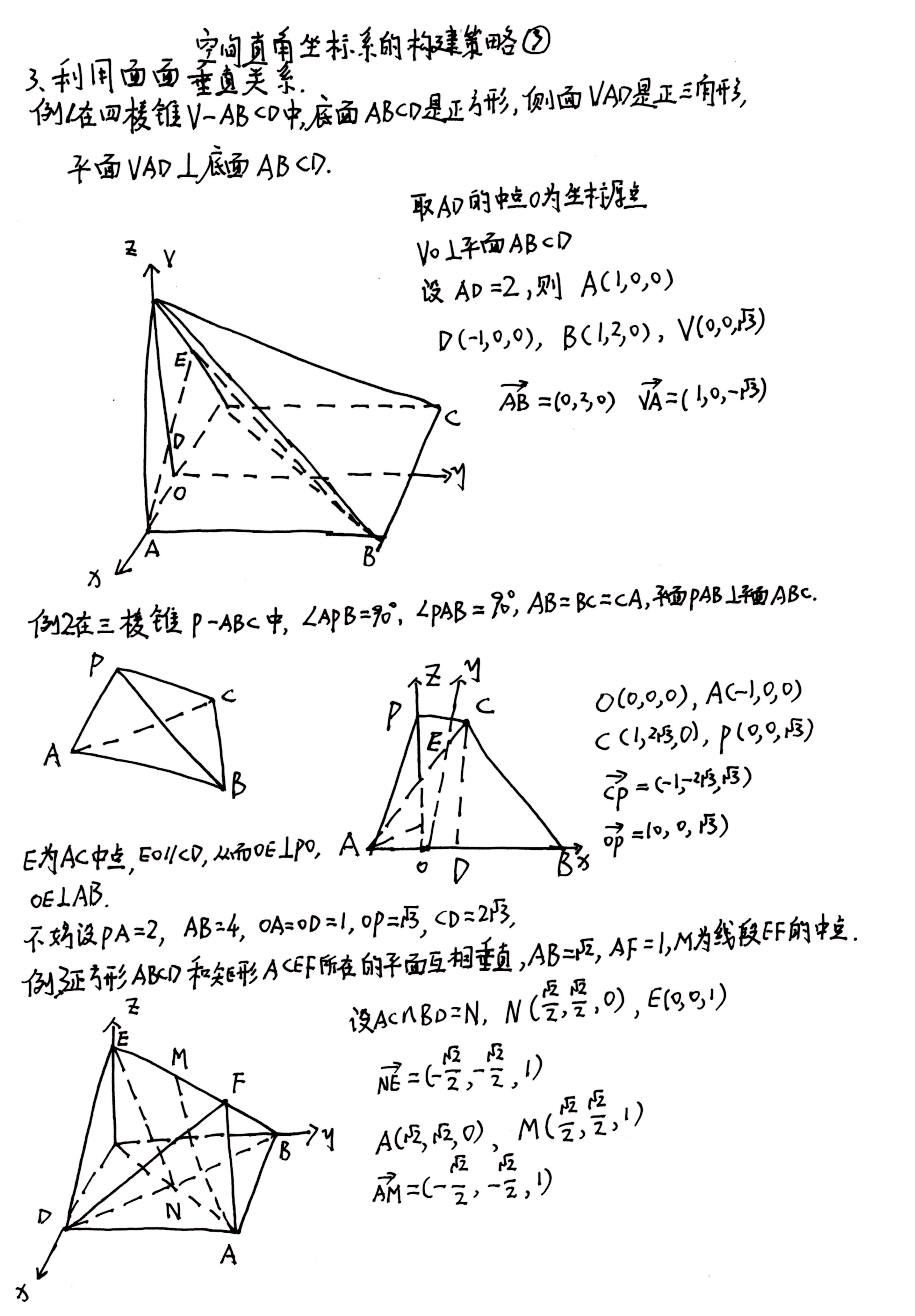
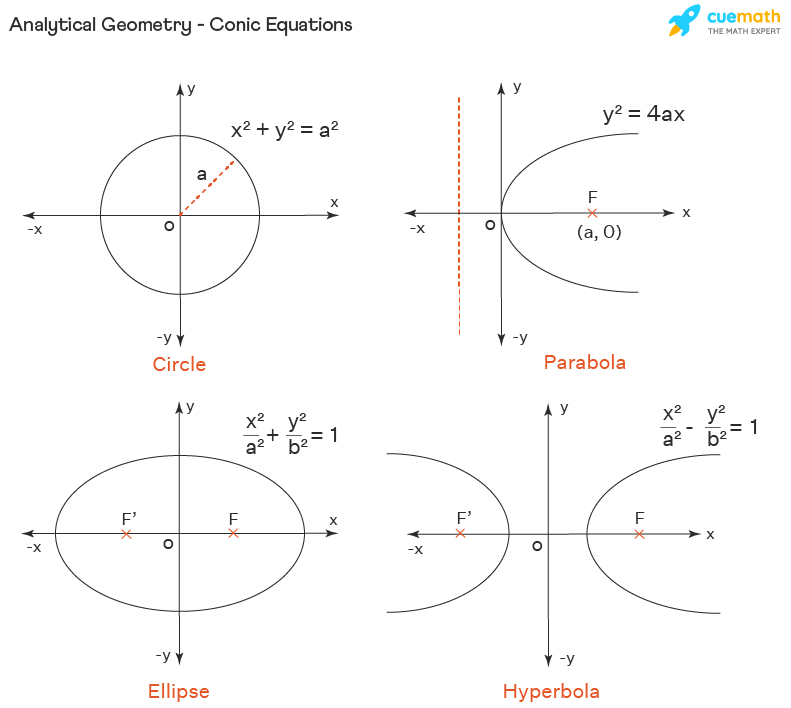
几何与代数看似毫无关联的两大数学分支,但实则内在联系甚深,需要我们换个角度去体会。

在大学的线性代数课程中,几何直观地解释了向量空间和变换的作用,如我之前文章中提到的,从子空间正交投影的几何意义分析方程组的解。

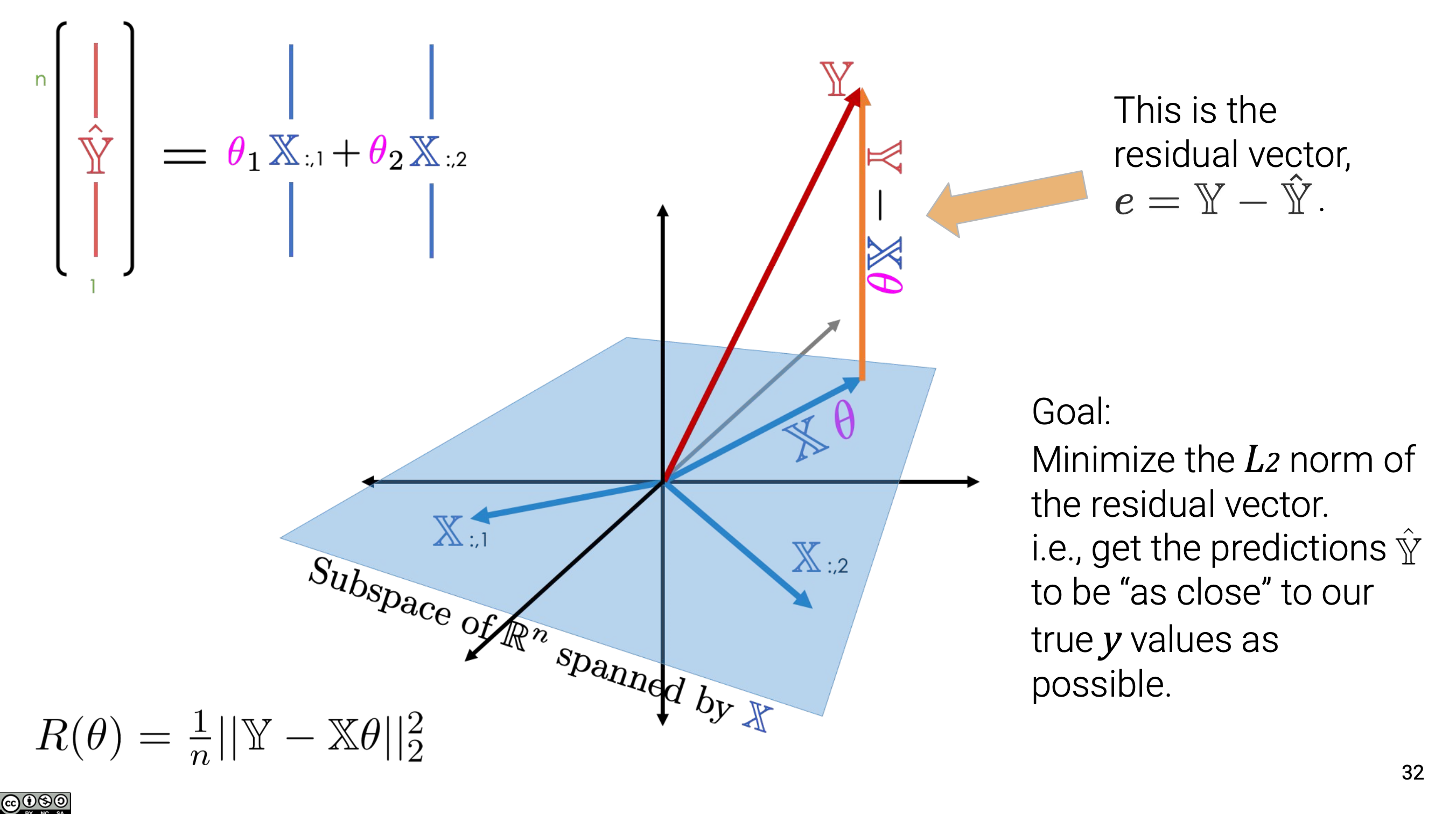
同样，有了初中对于概率计算和统计工具的初步认识后，在高中你将学习随机变量和概率分布等概念，你会接触四分数，峰度，偏度等高级的统计量。

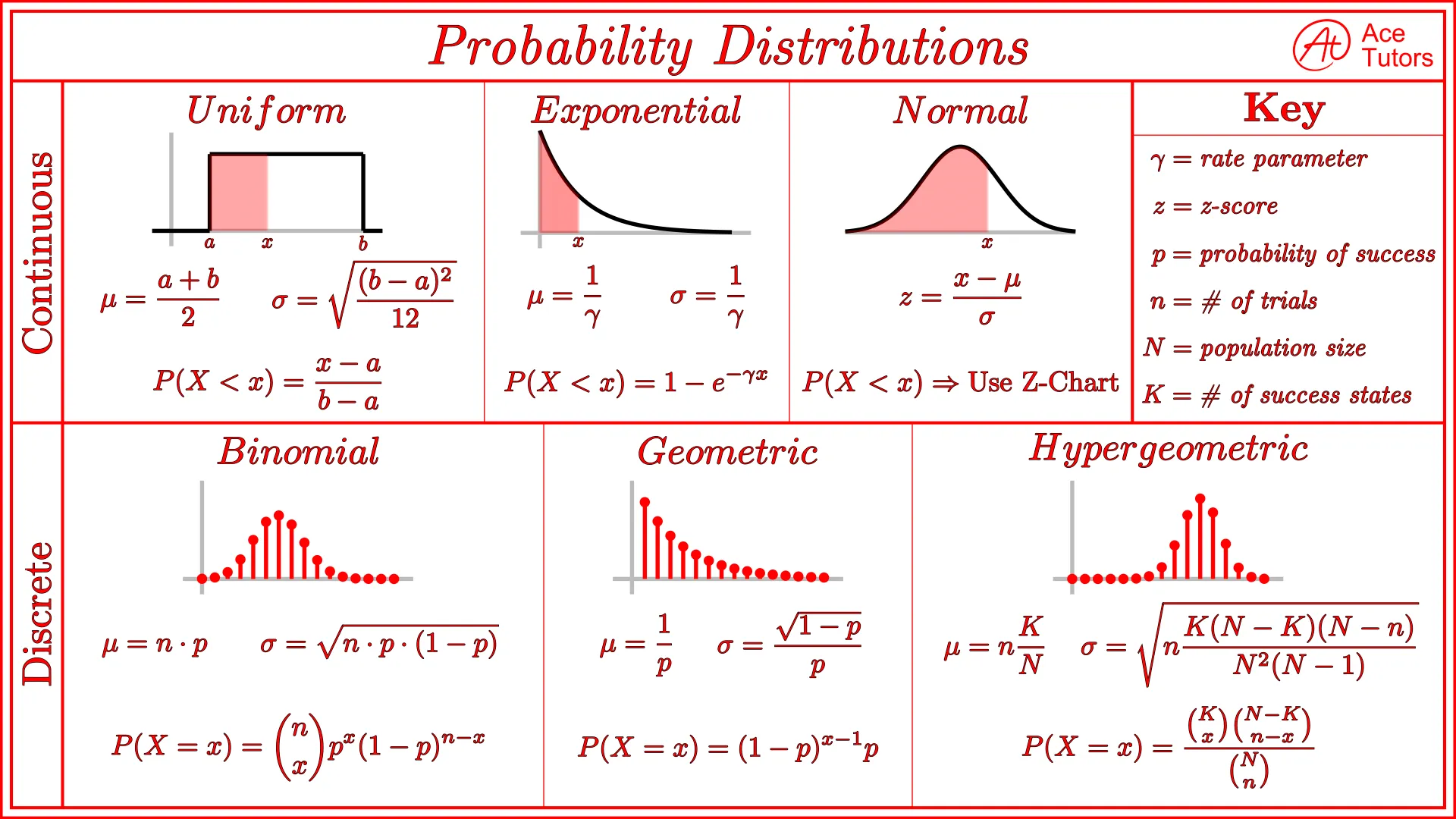
最后，你还会在高中学习数列的概念，数列是由一系列按照特定规律排列的数字组成的序列，包括等差数列、等比数列，其中还有大家所熟悉的斐波那契数列。

但是对于数列的用途，除了在各大公司的笔试题，数学竞赛中经常出现外，我还是没弄明白其实际意义，有可能是一种锻炼人思维模式的方法吧。

此时，你将迎来能改变人生命运的重大时刻：高考，之后你会进入大学生活。

因为高考后，有的人会选择数学专业，数学专业所学的内容和非数学专业有很大区别。

即使是同一个专业，根据专业的不同，不同院校开设的数学课程也不尽相同。

所以，无法叙述详尽。

大学数学

但大一的第一门数学课一定是高等数学，在大学之前学的数学都离不开”理想情况下”的假设。

• 几何里的点没有体积,线没有宽度,面没有厚度

• 所有的函数都具有连续性

• 统计数据符合正态分布

• 概率问题中事件都是等可能的，独立同分布的。

• 所有集合都清晰定义

• 方程是单变量，且有精确解。

• 函数只有有限个自变量，且都是凸函数。

。。。

但现实是残酷的，哪有那么多理想的假设。

在高等数学中我们将面临更开放和复杂的环境。

• 函数可能不存在导数或不连续

• 数据分布严重偏态难以描述

• 元素难以明确定义或数量趋向无穷

所以在大学的高等数学中将学习极限、微积分、重积分、无穷级数、常微分方程等。

线性代数和概率与统计也是大多数学生的必修课。

在大学之前的代数课程中，方程往往都有唯一解，且变量的维度也是有限的，但在大学的线性代数中，将会扩展到更高维的空间，且方程的解也会存在多种情况：唯一解，不存在，和无穷多个解。

方程组的求解方法也不局限于高斯消元，还会用行列式去判断解的存在性，以及用逆矩阵以及更高级的矩阵分解进行求解。矩阵分解除了可以求解方程，还会用于降维，例如PCA。

另外，也会将线性代数融入更多的实际问题之中，例如，用机器学习中的特征向量，计算机视觉中用矩阵表示图像，Transformer中用矩阵乘法计算注意力，多模态中用于向量点积计算相似度等等。

概率论与数理统计的内容也将变得更加深奥，从小样本到大样本复杂数据的统计分析；概率分布也从简单的均匀分布，正太分布扩展到更复杂的分布；同时也会讲解更复杂的分析工具：参数估计、假设检验、回归分析等。

好了，至此你学有所成，可以去谋取一份工作，并将所学应用于实践。

当然，如果你想继续深造考研读博时，则会学习更复杂的数学课程，因为我没有这个经历，所以只罗列在网上的搜索结果供大家参考。

• 离散数学:集合论、图论、编码、数论、递归、组合数学等 Discrete 数学知识。计算机专业必修课。

• 抽象代数:群论、环论、字段论、同态映射等抽象algebra系统的研究。部分理工科选修。

• 拓扑学:开集、闭集、度量空间、连通性、紧致性等拓扑性质的研究。大部分为理工科高年级选修课。

好了，到此，我已经帮你罗列了从小学到大学的数学课程。

每个阶段的数学知识，从素质教育的角度看，有两个目的，一是应用所学的知识解决当时的认知水平下的问题，另一个是衔接下一个阶段的数学课程，为下一个阶段的课程做铺垫，打地基。

素质教育不再是逼着学生死记硬背，而是鼓励将其应用到日常生活中。

而从应试教育的角度看，目的只有一个，就是得高分，考好的学校。

我们国家和西方国家在教育方面的差别在于，西方国家真正做到了因材施教，也就是让不热爱数学的学生接受最普通的数学教育，而让喜欢数学的学生接受顶尖的数学教育。

这就是为什么我们学生考分比他们高，却做不出牛逼的东西。

除此之外，数学是否能够对人生有所启发，我就没有能力去评论了。

那么我为什么说数学是个谜？因为它就在你身边而不知。

数学的历史

让我们穿越时空，回顾古代至现代的数学发展：

古代数学：

• 埃及数学（公元前3000年前后）：应用于工程测量的简单加减法计算。

• 美索不达米亚数学（公元前1800年前后）：使用六十进位制，解二次二项式方程。

• 古印度数学（公元前1000年前后）：使用十进位制，提出质数概念，涉猎天文学和代数学术著作。

• 古希腊数学（公元前600年前后）：欧几里得编撰《几何原本》，建立公理化演绎体系基础。

中世纪数学：

• 阿拉伯数学（8-15世纪）：阿尔花拉兹密的《代数学全书》，奥马尔·海亚姆的三次方程解法。

• 中世纪欧洲数学（5-15世纪）：出现符号代数，菲波那契的《计算书》。

近代数学（17-19世纪）：

• 微积分的发展：牛顿与莱布尼茨独立发明微积分，解决了运动和变化问题。

• 非欧几何学：波恩不等式的发现否定了欧几里得公设，非欧几何学应运而生。

• 实数理论：底勒贝格提出完备性理论，建立实数体系。

• 群论：伽罗瓦理论奠基了抽象代数。

• 概率论：拉普拉斯对概率论作出重要贡献。

现代数学（20世纪至今）：

• 集合论：康托尔严格定义集合概念，戈德尔提出不完备定理。

• 拓扑学：豪斯多夫创立点集拓扑学。

• 计算机科学：图灵提出图灵机，关联算法理论与计算复杂度。

也难怪是个谜，看看数学的历史，然后再与你所学的内容做个对比，你就会发现你所学的内容和整个数学领域所包含的内容相比，确实是沧海一粟。

数学的分支

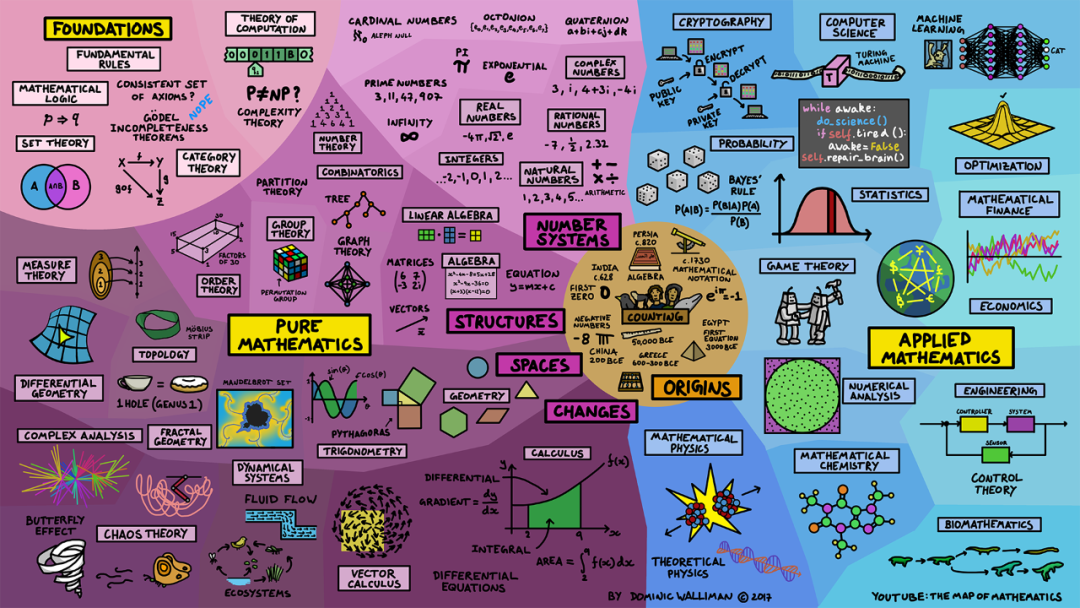
数学起源于计数

人类计数(count)可以追溯到史前时代，人们在骨头上刻画记号。随着时间的推移，数学发生了几次创新，埃及人首次提出了方程，古希腊人在几何学和数理数学等许多领域取得了重大进展，负数在中国发明，零作为一个数字最早在印度使用。

这个时期我们称之为古代数学(约前3000年-约前300年)，这里给大家一个时间上的参照，古希腊人毕达哥拉斯提出勾股定理时我国正处于春秋战国时期。

然后，在伊斯兰黄金时代，波斯数学家取得了进一步的发展，第一本代数学著作被写成。这个时期也被称为中世纪数学(约500年-1400年)，而此时中国正在跨越唐宋元明等朝代。

然后，在文艺复兴时期，数学与科学一起蓬勃发展。解析几何、微积分的创立。出现了对数、概率论等分支。这个时期我们也称为近代数学(17世纪-19世纪)，而此时的中国正处于没落的大清王朝。

而我们主要关注现代数学(20世纪至今)。

数学的两大分支

现代数学可以大致分为两个领域，左侧的纯数学(Pure Mathematics)和右侧的应用数学(Appiled Mathematics)。

纯数学研究数学本身，而应用数学则是为了解决现实世界的问题。但两者之间并非泾渭分明。很多科学家在其所在的领域科研时发现一些古老的纯数学理论正是他们解决现实世界问题所需要的，即使时间跨度几个世纪，抽象的东西最终变得非常有用。

好了，让我们开始进入正题，纯数学由几个部分组成。

数字系统(Number Systems)

数字的研究从自然数(Natural Numbers)开始，以及你可以用它们做什么，例如算术运算(Arithmetic)，然后研究其他类型的数字，如整数(Integer)（包括负数）、有理数(Rational Numbers)（如分数）、实数(Real Numbers)（包括像π这样的无限小数）以及复数(Complex Numbers)等等。以及一些具有有趣的特性的数字，如素数、π或指数。

结构(Structures)

研究结构的学科是从将数字放入变量形式的方程式开始，代数(Algebra)包含了处理这些方程式的规则。在代数中，你还会找到向量(Vector)和矩阵(Matrices)，它们之间的关系规则被捕捉在线性代数(Linear Algebra)中。

数论(Number Theory)研究数字系统中数字的特性，例如素数的性质。

组合学(Combinatorics)研究特定结构的性质，如树(Tree)、图(Graph)以及由离散块组成的其他事物。

群论(Group Theory)研究相互关联的对象，例如魔方是置换群的一个例子。

序理论(order theory)研究如何按照一定的规则排列对象。自然数就是有序对象的一个例子。

空间(Space)与形状(Shape)

纯数学的另一个部分研究形状(Shape)及其在空间(Space)中的行为。

起源于几何学(Geometry)，其中包括与三角学(trigonometry)密切相关的毕达哥拉斯学派，如果说毕达哥拉斯定理你不知道，那换个称呼勾股定理你一定很熟悉。

还有一些有趣的东西，例如分形几何(Fractal Geometry)，它是一种数学模式，具有尺度不变性，这意味着你可以无限缩放它们，它们看起来总是差不多的。

拓扑学(Topology)研究允许连续变形但不允许撕裂或粘合的空间的不同属性。例如，咖啡杯和甜甜圈在拓扑上是相同的。

测度论(Measure Theory)是一种给空间或集合分配值的方法，将数字和空间联系在一起。

最后，微分几何(Differential Geometry)研究曲面上形状的性质。例如，在曲面上，三角形的角度是不同的。

变化(changes)

接下来我们来到下一个部分，即变化(changes)。

研究变化的学科包括微积分(calculus)，涉及到积分(integrals)和微分(differentials)。微积分研究函数所围成的面积或函数梯度(gradients)的行为。而矢量微积分(vector calculus)则研究同样的内容，但针对矢量进行分析。

在这里，我们还会涉及到一系列其他领域，如动态系统(dynamical systems)，它研究随时间从一个状态演变到另一个状态的系统，例如流体流动(fluid flows)或具有反馈环路的生态系统(ecosystems)和混沌理论(chaos theory)，它研究对初始条件非常敏感的动力系统。

最后，复分析(complex analysis)研究具有复数的函数的性质。

应用数学：百花齐放

我们将从物理学(physics)开始，它在某种程度上使用了左边几乎所有的内容。数学和理论物理学(theoretical physics)之间有着非常密切的关系。

数学也在其他自然科学中得到应用，包括数学化学(mathematical chemistry)和生物数学(biomathematics)，它们研究了从分子建模到进化生物学等各种内容。

数学在工程学(engineering)中也被广泛应用。自从古埃及和巴比伦时代以来，建造事物就需要大量的数学知识。非常复杂的电气系统，例如飞机或电力网络，使用了动力系统中的控制理论(control theory)方法。

数值分析(numerical analysis)是一种数学工具，通常在数学变得过于复杂无法完全解决的情况下使用。因此，我们会使用许多简单的近似方法，并将它们组合在一起，以获得良好的近似答案。例如，如果你把一个圆放在一个正方形内，然后向它投掷飞镖，然后比较圆内和正方形部分的飞镖数量，你可以近似计算出圆周率的值。但在现实世界中，数值分析是在大型计算机上进行的。

博弈论(game theory)研究在给定一组规则和理性玩家的情况下，最佳选择是什么，并且它在经济学(economics)中使用。

概率论(probability)是研究随机事件的学科，例如抛硬币、掷骰子或人类行为。

统计学(statistics)是研究大量随机过程或数据组织和分析的学科。

这显然与数学金融(mathematical finance)相关，您希望对金融系统建模并获得优势，以赢得丰厚的回报。

与回报相关的是优化(optimization)，您试图在众多不同选项或约束条件中计算出最佳选择，通常将其视为寻找函数最高点或最低点。优化问题对我们人类来说是第二天性，我们经常进行这样的计算，试图在某种方式上获得最佳性价比或最大化幸福感。

与纯数学密切相关的另一个领域是计算机科学(computer science)。计算机科学的规则实际上是从纯数学中推导出来的，这是一个在可编程计算机出现之前就被研究出来的例子。

机器学习(machine learning)是创建智能计算机系统的过程，它使用了线性代数、优化、动力系统和概率等数学领域的许多方法。

最后，密码学(cryptography)理论对计算非常重要，它使用了许多纯数学方法，如组合数学和数论。

AI中的数学

最后，回到我们的主题。

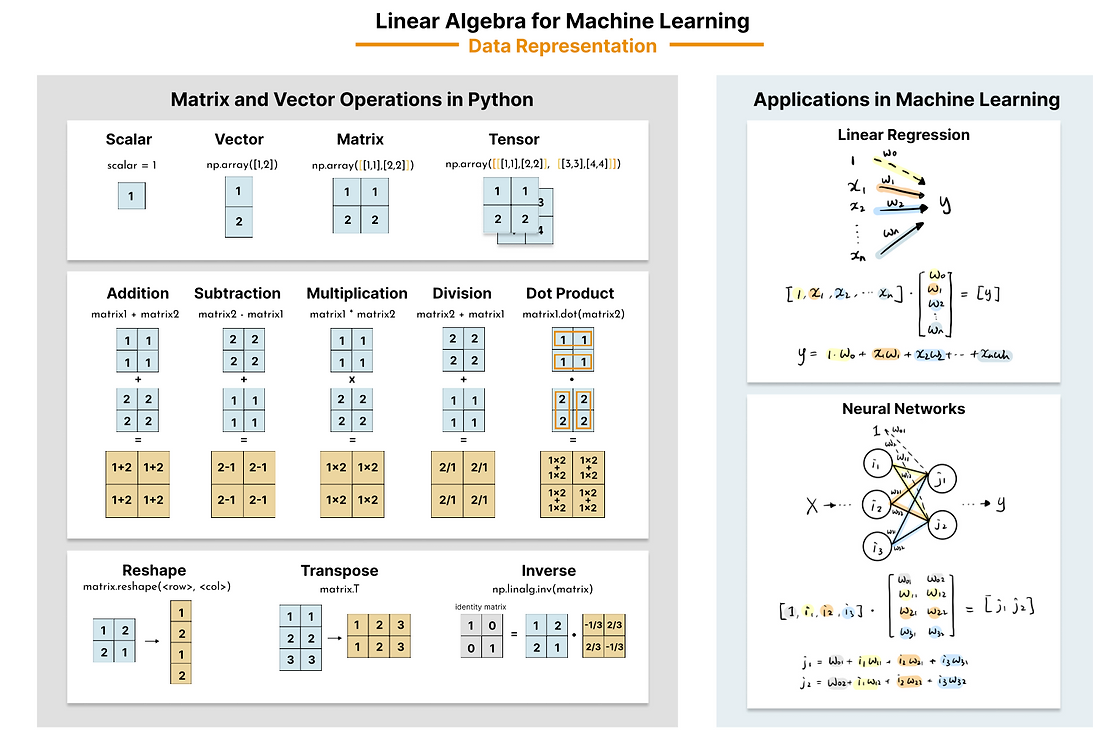
线性代数：线性代数是研究向量空间、线性变换和矩阵运算的数学学科，在AI中广泛应用于矩阵计算、向量空间模型以及线性回归等方面。

概率与统计：概率与统计是研究随机事件和数据分析的数学分支，它在AI中的应用包括机器学习算法的建模与评估、数据预处理、概率图模型以及决策理论等。

微积分：微积分是研究函数、极限、导数和积分等数学工具，它在AI中的应用涵盖了优化算法、神经网络的训练与优化、梯度下降、函数拟合等领域。

优化算法：优化算法是解决最优化问题的方法，它在AI中的应用包括模型参数优化、神经网络训练、特征选择、超参数调整等方面，用于寻找最佳解或最优策略。

数学是个谜，也是个迷​。